题目描述 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
1 2 输入: [3,2,1,5,6,4], k = 2 输出: 5
具体见题目详解 。
算法思路 这个题目要求 O(n)复杂度排序,这个其实很难想得到,一般的排序都是 $O(n^2)$或者$O(nlog_2n)$,能达到$O(n)$的只有基数排序,桶排序 等等非比较算法,我首先借鉴了个桶排序算法,其主要思路是分治 和快排 思路 。代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { void bucketSort (vector<int >& nums, int bucketSize) if (nums.empty ()) return ; int minValue = *min_element (nums.begin (), nums.end ()); int maxValue = *max_element (nums.begin (), nums.end ()); vector< vector<int > > buckets ((maxValue - minValue) / bucketSize + 1 ); for (int num : nums) { buckets[(num - minValue) / bucketSize].push_back (num); } for (auto & bucket : buckets) { sort (bucket.begin (), bucket.end ()); } int index = 0 ; for (auto & bucket : buckets) { for (int num : bucket) { nums[index++] = num; } } } public : int findKthLargest (vector<int >& nums, int k) int numsOfbarrel = (int )sqrt (nums.size ()); bucketSort (nums, numsOfbarrel); return nums[nums.size () - k]; } };
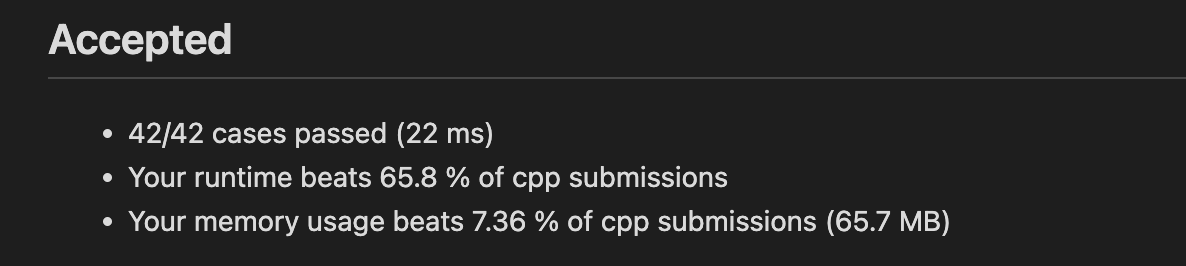
算法结果如下,看样子并不是很快:
桶排序也很取决于数据的分布程度是否均匀、桶的数量 如何等等。我这种菜狗写不出来足够快的桶排序。
借鉴思路 方法1-快速选择 第一种方法其实上课讲过,不过后来我算法课中期退课了(因为cb实在是天雷 ,如果学弟学妹有幸看到一定壁垒,还好我跑得快……)。
这个快速选择是基于快速排序的基础上的,首先我们需要知道什么是快速排序,大概是这样的:
对于一个数组nums,任意选定一个轴x,使得对于i, j œ [0, len(nums) - 1]的所有元素,其需要进行交换移位,满足:
若nums[i]大于nums[x], nums[j]小于nums[x],则交换nums[i], nums[j]的位置。
也就是说,在交换完毕之后,x左侧的元素都需要小于nums[x] ,x右侧的元素需要大于nums[x] 。
我讲的比较抽象,具体可以看上面的csdn-blog。但是这样其实还不是最快的,因为上面的核心思路:x的左侧元素小于nums[x],右侧元素大于nums[x] ,如果这个x就是k,那不就找到这个k了吗,我们并不关心左右侧元素是否有序,只需要知道nums[k]就是第k个大的元素。代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int quickselect (vector<int > &nums, int l, int r, int k) if (l == r) return nums[k]; int partition = nums[l], i = l - 1 , j = r + 1 ; while (i < j) { do i++; while (nums[i] < partition); do j--; while (nums[j] > partition); if (i < j) swap (nums[i], nums[j]); } if (k <= j)return quickselect (nums, l, j, k); else return quickselect (nums, j + 1 , r, k); } int findKthLargest (vector<int > &nums, int k) int n = nums.size (); return quickselect (nums, 0 , n - 1 , n - k); } };
更具体的可以看官方题解 ,写得也很好。