HOT100-6-最大正方形
题目描述
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:

1 | 输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] |
算法思路
这道题目很明显我是不会的!我只能暴力求解,主要思路是:对于matrix[i][j],将其作为正方形的左上角,遍历寻找最大的正方形,复杂度是 O(mn*min(m, n)),这也不算是算法了,就不在这里展示。
借鉴思路
这里看了官方题解,只觉得会的题就是会,不会就是不会,dp在这道题目里真是用的淋漓尽致了。算法思路是:
要想求出 最大正方形面积,就需要求出 最大正方形边长,最后的面积就是边长的平方。
我们记
dp[i][j]为以matrix[i][j]为正方形右下角时最大的正方形边长,那么很容易有:- 若
matrix[i][j] = 0,dp[i][j] = 0 若
matrix[i][j] = 1,dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1,这个证明需要画一张图理解,其实很容易,但是真正想起来是很困难的。我们借鉴这个优秀题解的图片。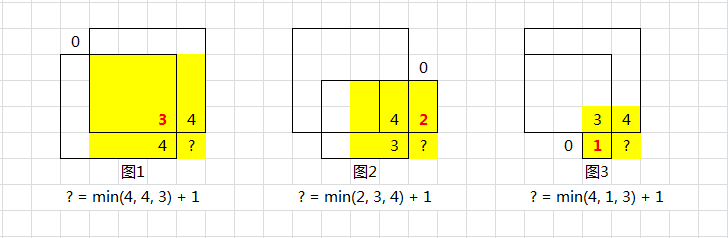
- 若
取
maxLength = max(maxLength, dp[i][j])即可。
代码如下:
1 | class Solution { |
我尝试了一下vector发现速率其实不如内置数组,能实现的最高效率也就是这样了,最后需要安全释放指针(软安学多了…..)。
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
